Recently I have been complaining about the low standards to which science has sunk. It has become normal to be surprised by an observation, express doubt about the data, blame the observers, slowly let it sink in, bicker and argue for a while, construct an unsatisfactory model that sort-of, kind-of explains the surprising data but not really, call it natural, then pretend like that’s what we expected all along. This has been going on for so long that younger scientists might be forgiven if they think this is how science is suppose to work. It is not.
At the root of the scientific method is hypothesis testing through prediction and subsequent observation. Ideally, the prediction comes before the experiment. The highest standard is a prediction made before the fact in ignorance of the ultimate result. This is incontrovertibly superior to post-hoc fits and hand-waving explanations: it is how we’re suppose to avoid playing favorites.
I predicted the velocity dispersion of Crater 2 in advance of the observation, for both ΛCDM and MOND. The prediction for MOND is reasonably straightforward. That for ΛCDM is fraught. There is no agreed method by which to do this, and it may be that the real prediction is that this sort of thing is not possible to predict.
The reason it is difficult to predict the velocity dispersions of specific, individual dwarf satellite galaxies in ΛCDM is that the stellar mass-halo mass relation must be strongly non-linear to reconcile the steep mass function of dark matter sub-halos with their small observed numbers. This is closely related to the M*-Mhalo relation found by abundance matching. The consequence is that the luminosity of dwarf satellites can change a lot for tiny changes in halo mass.
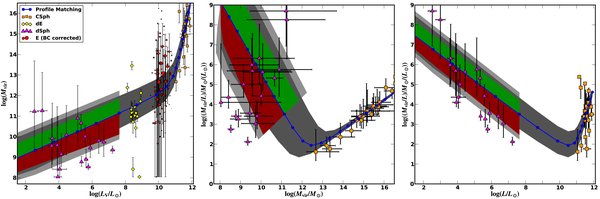
Long story short, the nominal expectation for ΛCDM is a lot of scatter. Photometrically identical dwarfs can live in halos with very different velocity dispersions. The trend between mass, luminosity, and velocity dispersion is so weak that it might barely be perceptible. The photometric data should not be predictive of the velocity dispersion.
It is hard to get even a ballpark answer that doesn’t make reference to other measurements. Empirically, there is some correlation between size and velocity dispersion. This “predicts” σ = 17 km/s. That is not a true theoretical prediction; it is just the application of data to anticipate other data.
Abundance matching relations provide a highly uncertain estimate. The first time I tried to do this, I got unphysical answers (σ = 0.1 km/s, which is less than the stars alone would cause without dark matter – about 0.5 km/s). The application of abundance matching requires extrapolation of fits to data at high mass to very low mass. Extrapolating the M*-Mhalo relation over many decades in mass is very sensitive to the low mass slope of the fitted relation, so it depends on which one you pick.

Since my first pick did not work, lets go with the value suggested to me by James Bullock: σ = 11 km/s. That is the mid-value (the blue lines in the figure above); the true value could easily scatter higher or lower. Very hard to predict with any precision. But given the luminosity and size of Crater 2, we expect numbers like 11 or 17 km/s.
The measured velocity dispersion is σ = 2.7 ± 0.3 km/s.
This is incredibly low. Shockingly so, considering the enormous size of the system (1 kpc half light radius). The NFW halos predicted by ΛCDM don’t do that.
To illustrate how far off this is, I have adopted this figure from Boylan-Kolchin et al. (2012).
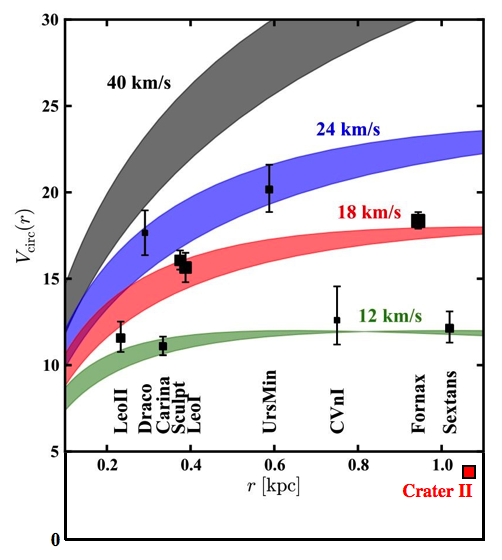
Basically, NFW halos, including the sub-halos imagined to host dwarf satellite galaxies, have rotation curves that rise rapidly and stay high in proportion to the cube root of the halo mass. This property makes it very challenging to explain a low velocity at a large radius: exactly the properties observed in Crater 2.
Lets not fail to appreciate how extremely wrong this is. The original version of the graph above stopped at 5 km/s. It didn’t extend to lower values because they were absurd. There was no reason to imagine that this would be possible. Indeed, the point of their paper was that the observed dwarf velocity dispersions were already too low. To get to lower velocity, you need an absurdly low mass sub-halo – around 107 M☉. In contrast, the usual inference of masses for sub-halos containing dwarfs of similar luminosity is around 109 M☉to 1010 M☉. So the low observed velocity dispersion – especially at such a large radius – seems nigh on impossible.
More generally, there is no way in ΛCDM to predict the velocity dispersions of particular individual dwarfs. There is too much intrinsic scatter in the highly non-linear relation between luminosity and halo mass. Given the photometry, all we can say is “somewhere in this ballpark.” Making an object-specific prediction is impossible.
Except that it is possible. I did it. In advance.
The predicted velocity dispersion is σ = 2.1 +0.9/-0.6 km/s.
I’m an equal opportunity scientist. In addition to ΛCDM, I also considered MOND. The successful prediction is that of MOND. (The quoted uncertainty reflects the uncertainty in the stellar mass-to-light ratio.) The difference is that MOND makes a specific prediction for every individual object. And it comes true. Again.
MOND is a funny theory. The amplitude of the mass discrepancy it induces depends on how low the acceleration of a system is. If Crater 2 were off by itself in the middle of intergalactic space, MOND would predict it should have a velocity dispersion of about 4 km/s.
But Crater 2 is not isolated. It is close enough to the Milky Way that there is an additional, external acceleration imposed by the Milky Way. The net result is that the acceleration isn’t quite as low as it would be were Crater 2 al by its lonesome. Consequently, the predicted velocity dispersion is a measly 2 km/s. As observed.
In MOND, this is called the External Field Effect (EFE). Theoretically, the EFE is rather disturbing, as it breaks the Strong Equivalence Principle. In particular, Local Position Invariance in gravitational experiments is violated: the velocity dispersion of a dwarf satellite depends on whether it is isolated from its host or not. Weak equivalence (the universality of free fall) and the Einstein Equivalence Principle (which excludes gravitational experiments) may still hold.
We identified several pairs of photometrically identical dwarfs around Andromeda. Some are subject to the EFE while others are not. We see the predicted effect of the EFE: isolated dwarfs have higher velocity dispersions than their twins afflicted by the EFE.
If it is just a matter of sub-halo mass, the current location of the dwarf should not matter. The velocity dispersion certainly should not depend on the bizarre MOND criterion for whether a dwarf is affected by the EFE or not. It isn’t a simple distance-dependency. It depends on the ratio of internal to external acceleration. A relatively dense dwarf might still behave as an isolated system close to its host, while a really diffuse one might be affected by the EFE even when very remote.
When Crater 2 was first discovered, I ground through the math and tweeted the prediction. I didn’t want to write a paper for just one object. However, I eventually did so because I realized that Crater 2 is important as an extreme example of a dwarf so diffuse that it is affected by the EFE despite being very remote (120 kpc from the Milky Way). This is not easy to reproduce any other way. Indeed, MOND with the EFE is the only way that I am aware of whereby it is possible to predict, in advance, the velocity dispersion of this particular dwarf.
If I put my ΛCDM hat back on, it gives me pause that any method can make this prediction. As discussed above, this shouldn’t be possible. There is too much intrinsic scatter in the halo mass-luminosity relation.
If we cook up an explanation for the radial acceleration relation, we still can’t make this prediction. The RAR fit we obtained empirically predicts 4 km/s. This is indistinguishable from MOND for isolated objects. But the RAR itself is just an empirical law – it provides no reason to expect deviations, nor how to predict them. MOND does both, does it right, and has done so before, repeatedly. In contrast, the acceleration of Crater 2 is below the minimum allowed in ΛCDM according to Navarro et al.
For these reasons I consider Crater 2 to be the bullet cluster of ΛCDM. Just as the bullet cluster seems like a straight-up contradiction to MOND, so too does Crater 2 for ΛCDM. It is something ΛCDM really can’t do. The difference is that you can just look at the bullet cluster. With Crater 2 you actually have to understand MOND as well as ΛCDM, and think it through.
So what can we do to save ΛCDM?
Whatever it takes, per usual.
One possibility is that Crater II may represent the “bright” tip of the extremely low surface brightness “stealth” fossils predicted by Bovill & Ricotti. Their predictions are encouraging for getting the size and surface brightness in the right ballpark. But I see no reason in this context to expect such a low velocity dispersion. They anticipate dispersions consistent with the ΛCDM discussion above, and correspondingly high mass-to-light ratios that are greater than observed for Crater 2 (M/L ≈ 104 rather than ~50).
A plausible suggestion I heard was from James Bullock. While noting that reionization should preclude the existence of galaxies in halos below 5 km/s, as we need for Crater 2, he suggested that tidal stripping could reduce an initially larger sub-halo to this point. I am dubious about this, as my impression from the simulations of Penarrubia was that the outer regions of the sub-halo were stripped first while leaving the inner regions (where the NFW cusp predicts high velocity dispersions) largely intact until near complete dissolution. In this context, it is important to bear in mind that the low velocity dispersion of Crater 2 is observed at large radii (1 kpc, not tens of pc). Still, I can imagine ways in which this might be made to work in this particular case, depending on its orbit. Tony Sohn has an HST program to measure the proper motion; this should constrain whether the object has ever passed close enough to the center of the Milky Way to have been tidally disrupted.
Josh Bland-Hawthorn pointed out to me that he made simulations that suggest a halo with a mass as low as 107 M☉ could make stars before reionization and retain them. This contradicts much of the conventional wisdom outlined above because they find a much lower (and in my opinion, more realistic) feedback efficiency for supernova feedback than assumed in most other simulations. If this is correct (as it may well be!) then it might explain Crater 2, but it would wreck all the feedback-based explanations given for all sorts of other things in ΛCDM, like the missing satellite problem and the cusp-core problem. We can’t have it both ways.

I’m sure people will come up with other clever ideas. These will inevitably be ad hoc suggestions cooked up in response to a previously inconceivable situation. This will ring hollow to me until we explain why MOND can predict anything right at all.
In the case of Crater 2, it isn’t just a matter of retrospectively explaining the radial acceleration relation. One also has to explain why exceptions to the RAR occur following the very specific, bizarre, and unique EFE formulation of MOND. If I could do that, I would have done so a long time ago.
No matter what we come up with, the best we can hope to do is a post facto explanation of something that MOND predicted correctly in advance. Can that be satisfactory?
Congratulations to the successful prediction. With MOND this is possible. You might be interested in the prediction of a Hercules-type satellite galaxy in 1997, 10 years before the discovery of the Hercules satellite in 2007. See Fig.6 in http://adsabs.harvard.edu/abs/2010A%26A…523A..32K. Once one leaves the LCDM framework, proper scientific work can resume.
LikeLike
I hesitate to comment, as I am way out of my depth here. But the external field effect seems to me to be an extremely important clue as to the nature of quantum gravity. At the end of the day, particle physicists need to find a graviton and until they do that, they are not qualified to comment on these issues. My take on the issue, as a mathematician, is that neutrinos permeate the universe, and do mediate a long-range force, which is either negligible, or is gravity. The latter option seems to me to be more reasonable, and I simply do not understand why no-one considers this possibility. Well, I do – they already “know” it is impossible. But they know this for theoretical reasons, not experimental ones, because gravitons “must” have spin 2, and neutrinos have spin 1/2. The theory is wrong – you have proved this experimentally, I have proved it mathematically. So now one can try to explain the external field effect in terms of neutrino oscillations. Anyone interested in collaborating on such a project? I know I can’t do it myself.
LikeLike